Abstract
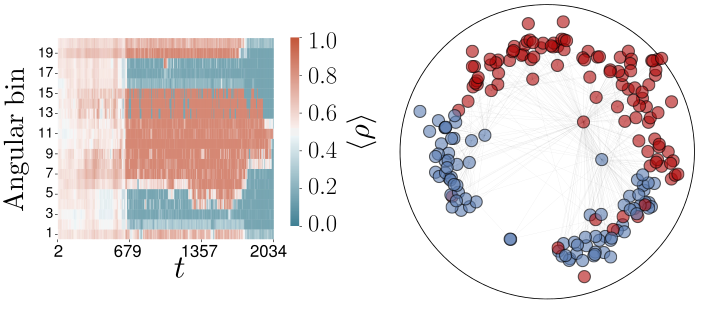
Despite group-level information is known to affect behavioural responses in social networks, very few models account for it. In this work we introduce the Multiscale Voter Model (MVM), that relies on network geometry to incorporate homophilic influences at different scales. We use numerical simulations to monitor the evolution of MVM dynamics in synthetic geometric networks and several real data sets. We identify a transition between a final stage of the dynamics with mixed binary opinions to one of full consensus, depending on the composition and size of the groups as well as their strength of influence. Strikingly, groups made of more diverse and less affine nodes promote eventual consensus. Contrarily, groups reflecting similarities between nodes, as captured by the latent geometry of the networks, yield to metastable clusters of same opinion which hinder the transition to general agreement. Finally, we study in detail the phenomenon of opinion segregation and discover that opinion clusters admit a visual interpretation. Spatial patterns observed in the underlying hyperbolic space of networks portray opinion domains and lead to new insights in opinion polarization dynamics.